Tr A Matrix

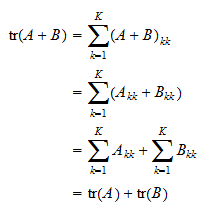
Tr a b 0 because tr ab tr ba and tr is linear.

Tr a matrix. 19 06 2020 tr function in r language is used to calculate the trace of a matrix. When both a and b are n n matrices the trace of the ring theoretic commutator of a and b vanishes. Tr j tr v 1 av tr vv 1 a tr i a tr a the canonical jordan form matrix j has the eigenvalues of a on its principal diagonal so the trace of j is equal to the sum of the eigenvalues of a. The matrix trace is implemented in the wolfram language as tr list.

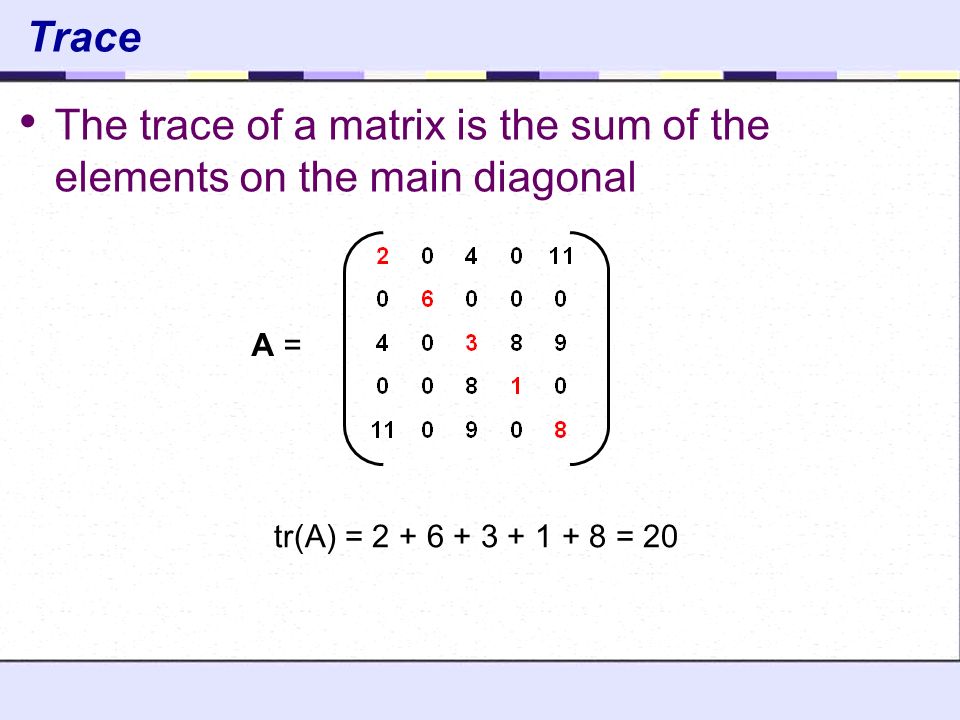
Trace of a matrix. The trace of a square matrix is the sum of its diagonal elements. Thus tr a σλ j. The sum of the diagonal elements of a square matrix.

By marco taboga phd. The trace of an n n square matrix a is defined to be tr a sum i 1 na ii 1 i e the sum of the diagonal elements. One can state this as the trace is a map of lie algebras gl n k from operators to scalars as the. By the definition of a trace of a matrix it follows that mathrm tr c 3 n 2 4.

That is the trace of a square matrix equals the sum of the eigenvalues counted with multiplicities. The tr function is used in various matrix operations and is the sum of the diagonal elements of a matrix. In group theory traces are known as group characters for square matrices a and b it is true that tr a tr a t 2 tr a b tr a tr b 3 tr alphaa alphatr a 4 lang 1987 p. The trace of a square matrix.

Before we look at what the trace of a matrix is let s first define what the main diagonal of a square matrix is.