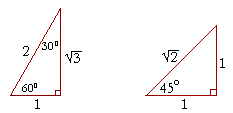Trigonometry 30 60 90 Degree Triangle

Triangle is that of the three sides that.

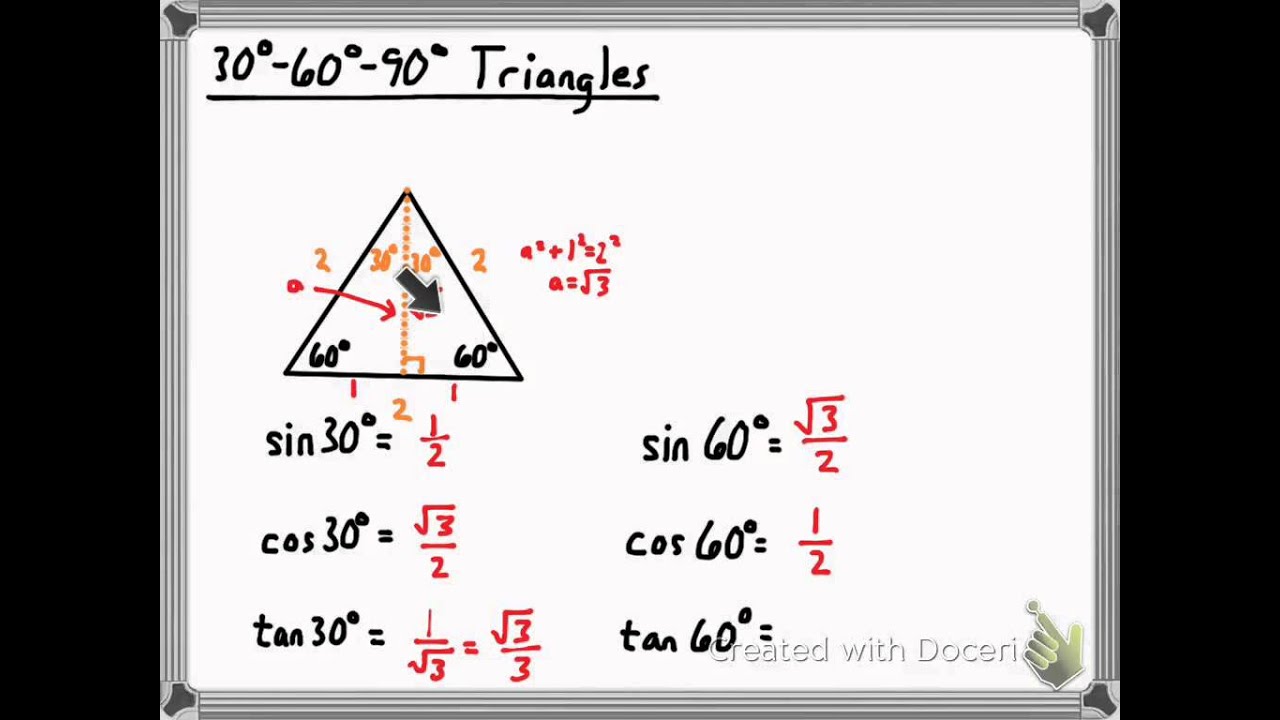
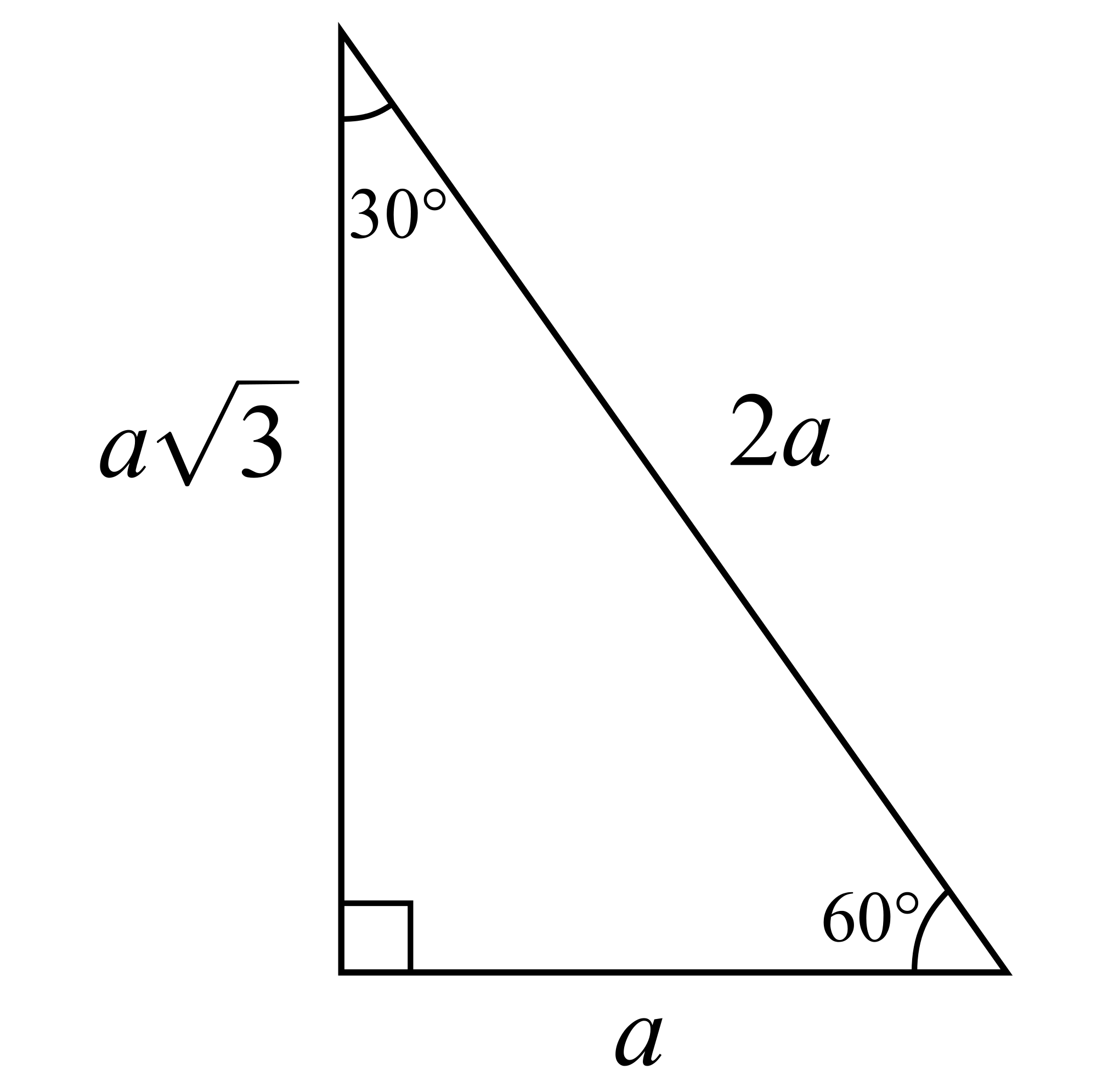
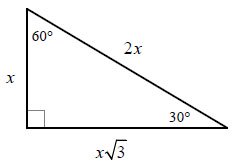
Trigonometry 30 60 90 degree triangle. Knowing these ratios makes it easy to compute the values of the trig functions for angles of 30 degrees π 6 and 60 degrees π 3. They are special because with simple geometry we can know the ratios of their sides. Also try 120 135 180 240 270 etc and notice that positions can be positive or negative by the rules of cartesian coordinates so the sine cosine and tangent change between positive and negative also. A 30 60 90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees.

90 and 30 60 90 triangles. So that s pretty amazing that of the three sides of a triangle when it s a 30 degree a 60 degree and a 90 degree i only need to know one side and. Because it is a special triangle it also has side length values which are always in a consistent relationship with one another. Now what s special about this 30 60 90.

Using these values in conjunction with reference angles and signs of the functions in the different quadrants you can determine the exact values of the multiples of these angles. Two of the most common right triangles are 30 60 90 and the 45 45 90 degree triangles all 30 60 90 triangles have sides with the same basic ratio if you look at the 30 60 90 degree triangle in radians it translates to the following. The 45 45 90 triangle also referred to as an isosceles right triangle since it has two sides of equal lengths is a right triangle in which the sides corresponding to the angles 45 45 90 follow a ratio of 1 1 2. Because it is a special triangle it also has side length values which are always in a consistent relationship with one another.

The most important rule to remember is that this special right triangle has one right angle and its sides are in an easy to remember consistent relationship with one another the ratio is a. Like the 30 60 90 triangle knowing one side length allows you to determine the lengths of the other sides. The hypotenuse is the longest side in a right triangle which is different from the long leg. A 30 60 90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees.

There are two special triangles in trigonometry. The other is the isosceles right triangle. Using the lengths of the sides of the two special right triangles the 30 60 90 right triangle and the 45 45 90 right triangle the following exact values for trig functions are found. The long leg is the leg opposite the 60 degree angle.

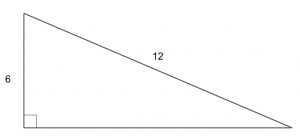
30 60 90 triangle rules and properties. In a 30 60 90 triangle the sides are in the ratio 1. We will prove that below. Play with this for a while move the mouse around and get familiar with values of sine cosine and tangent for different angles such as 0 30 45 60 and 90.

Are all going to be different i only need to know one and i can find the other two.